深度学习总结
神经网络基础
激活函数
激活函数是连接感知机和神经网络的桥梁,在神经网络中起着至关重要的作用。
如果没有激活函数,整个神经网络就等效于单层线性变换,不论如何加深层数,总是存 在与之等效的“无隐藏层的神经网络”。激活函数必须是非线性函数,也正是激活函数的存 在为神经网络引入了非线性,使得神经网络能够学习和表示复杂的非线性关系。
阶跃(Binary step)函数
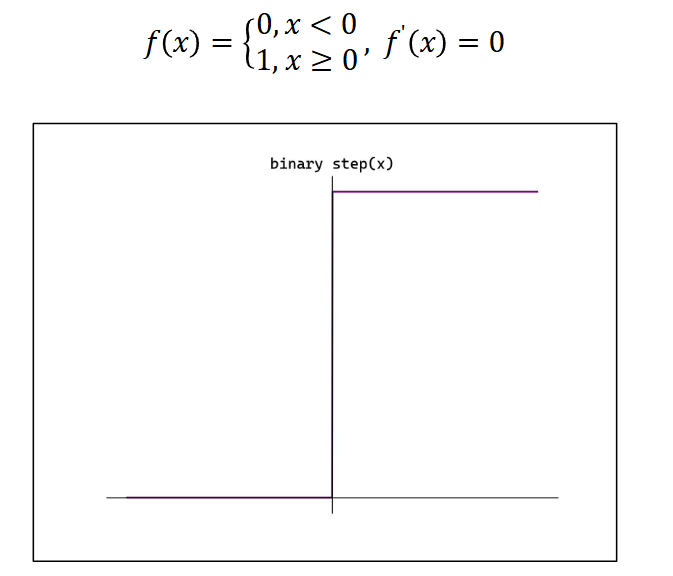
阶跃函数的导数恒为 0
Sigmoid 函数
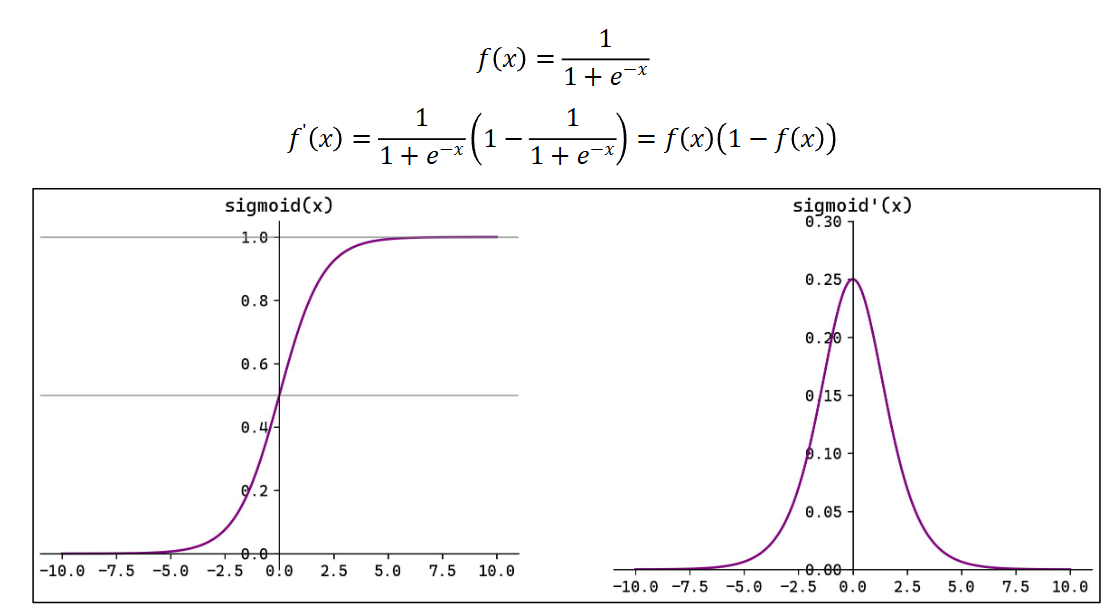
Sigmoid(也叫 Logistic 函数)是平滑的、可微的,能将任意输入映射到区间(0,1)。常 用于二分类的输出层。但因其涉及指数运算,计算量相对较高。
Sigmoid 的输入在[-6,6]之外时,其输出值变化很小,可能导致信息丢失。
Sigmoid 的输出并非以 0 为中心,其输出值均>0,导致后续层的输入始终为正,可能 影响后续梯度更新方向。
Sigmoid 的导数范围为(0,0.25),梯度较小。当输入在[-6,6]之外时,导数接近 0,此时网 络参数的更新将会极其缓慢。使用 Sigmoid 作为激活函数,可能出现梯度消失(在逐层反向 传播时,梯度会呈指数级衰减)。
Tanh 函数
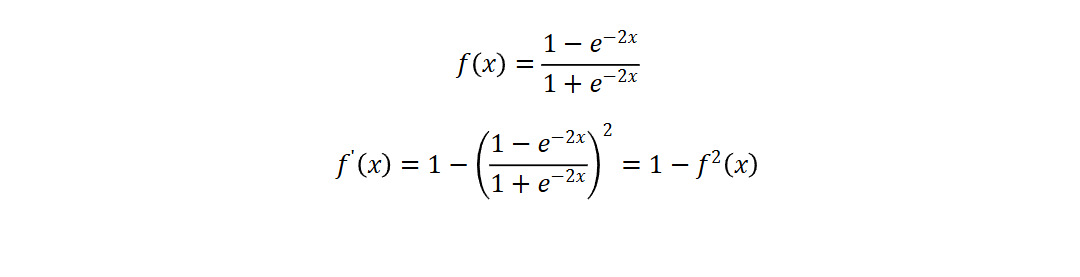
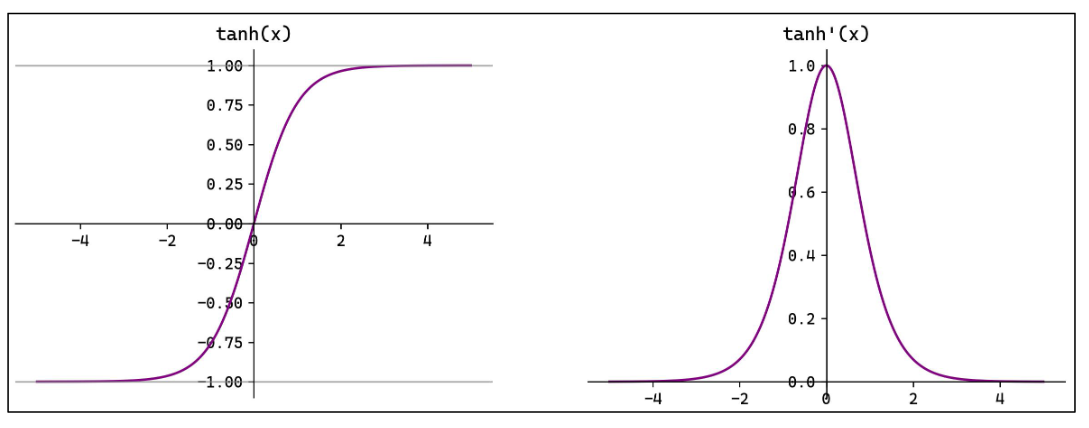
Tanh(双曲正切)将输入映射到区间(-1,1)。其关于原点中心对称。常用在隐藏层。
输入在[-3,3]之外时,Tanh 的输出值变化很小,此时其导数接近 0。
Tanh 的输出以 0 为中心,且其梯度相较于 Sigmoid 更大,收敛速度相对更快。但同样 也存在梯度消失现象。
ReLU 函数
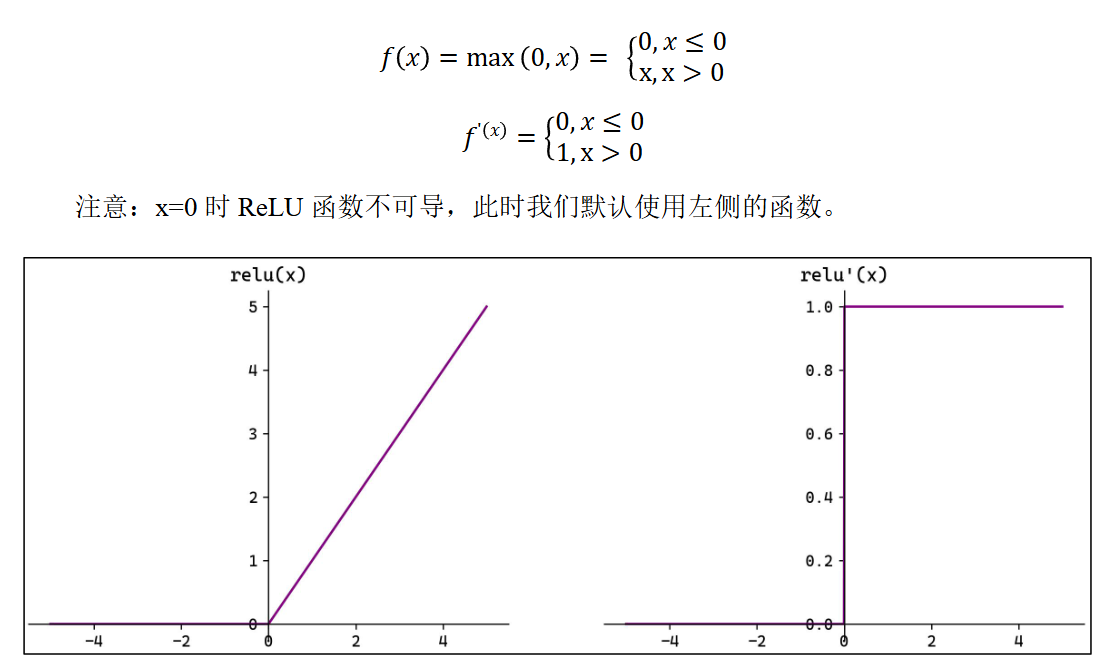
ReLU(Rectified Linear Unit,修正线性单元)会将小于 0 的输入转换为 0,大于等于 0 的输入则保持不变。 ReLU 定义简单,计算量小。常用于隐藏层。 ReLU 作为激活函数不存在梯度消失。当输入小于 0 时,ReLU 的输出为 0,这意味着 在神经网络中,ReLU 激活的节点只有部分是“活跃”的,这种稀疏性有助于减少计算量和 提高模型的效率。
当神经元的输入持续为负数时,ReLU 的输出始终为 0。这意味着神经元可能永远不会 被激活,从而导致“神经元死亡”问题。这会影响模型的学习能力,特别是如果大量的神经 元都变成了“死神经元”。为解决此问题,可使用 Leaky ReLU 来代替 ReLU 作为激活函数。 Leaky ReLU αx, x ≤ 0,其中α是一个很小的常数 在负数区域引入一个小的斜率来 解决“神经元死亡”问题。
Softmax 函数
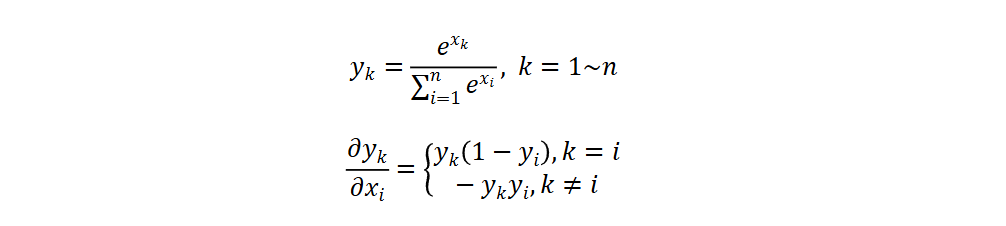
Softmax 将一个任意的实数向量转换为一个概率分布,确保输出值的总和为 1,是二分类 激活函数 Sigmoid 在多分类上的推广。
Softmax 常用于多分类问题的输出层,用来表示类别 的预测概率。 Softmax 会放大输入中较大的值,使得最大输入值对应的输出概率较大,其他较小的值 会被压缩。即在类别之间起到了一定的区分作用。
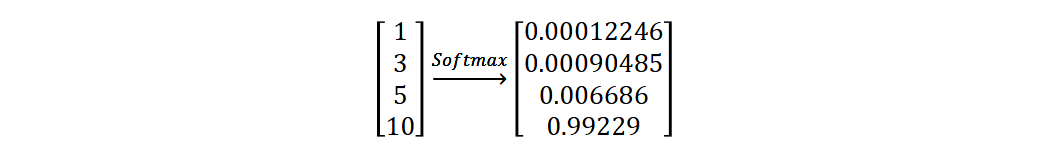
其他常见激活函数
Identity(恒等函数)
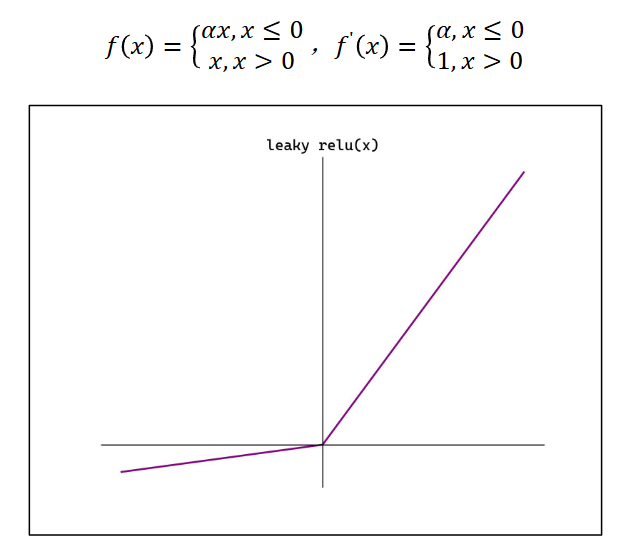
Leaky ReLU
Leaky Rectified Linear Unit
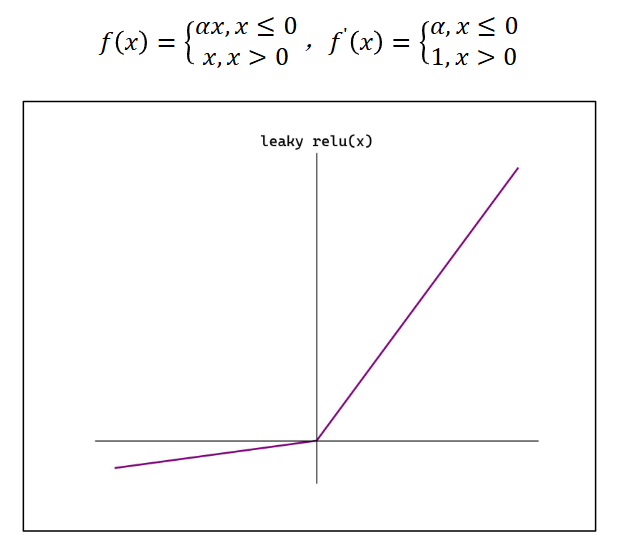
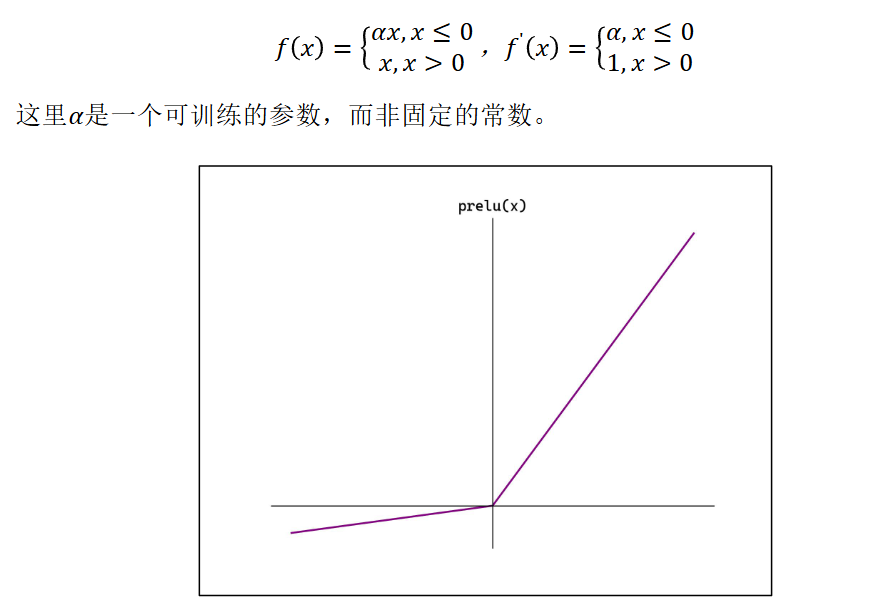
PReLU
Parametric Rectified Linear Unit
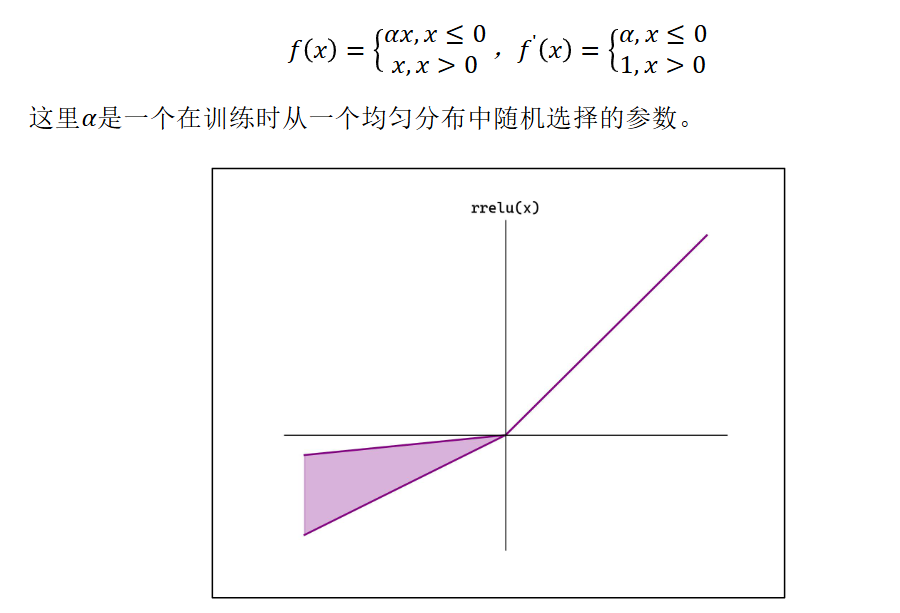
RReLU
Randomized Leaky ReLU
ELU
Exponential Linear Unit
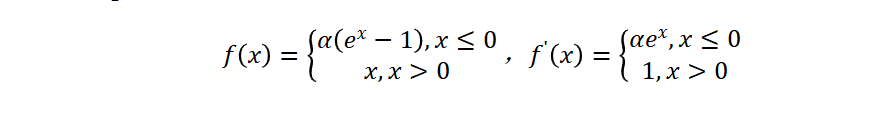
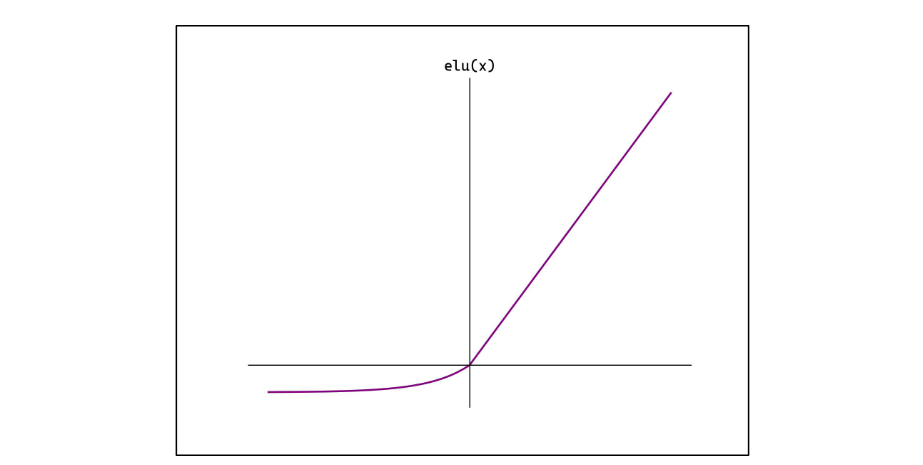
Swish
也称 Sigmoid Linear Unit,SiLU
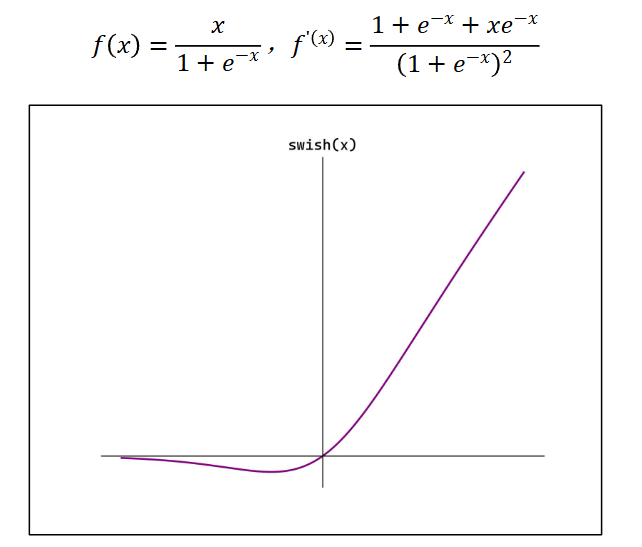
Softplus
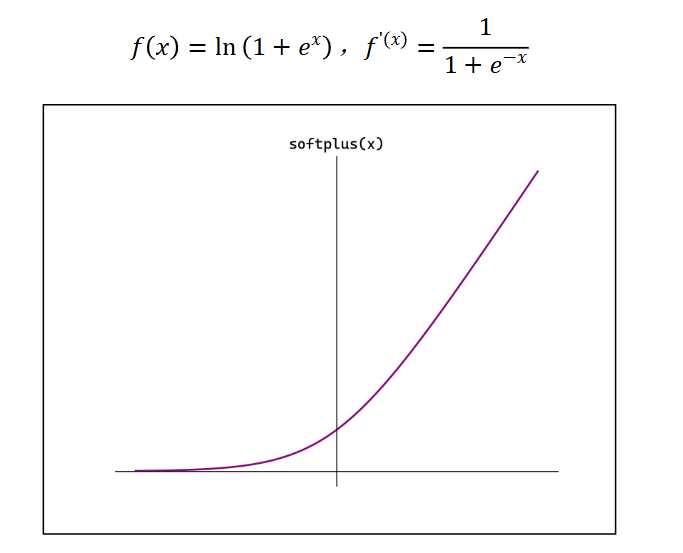
如何选择激活函数
隐藏层
首选 ReLU,如果效果不好可尝试 Leaky ReLU 等
Sigmoid 在隐藏层易导致梯度消失,应尽量避免
Tanh 的输出均值为 0,对中心化数据更友好,但仍可能引发梯度消失,仅适用于浅层网络
输出层
- 二分类选择 Sigmoid
- 多分类选择 Softmax
- 回归默认选择 Identity
神经网络的学习
损失函数
常见损失函数
均方误差(Mean Squared Error ,MSE),也称 L2 Loss:

交叉熵误差

分类任务损失函数
二分类任务损失函数

多分类任务损失函数

回归任务损失函数
平均绝对误差(Mean Absolute Erro,MAE),也称 L1 Loss
均方误差(Mean Squared Error ,MSE),也称 L2 Loss
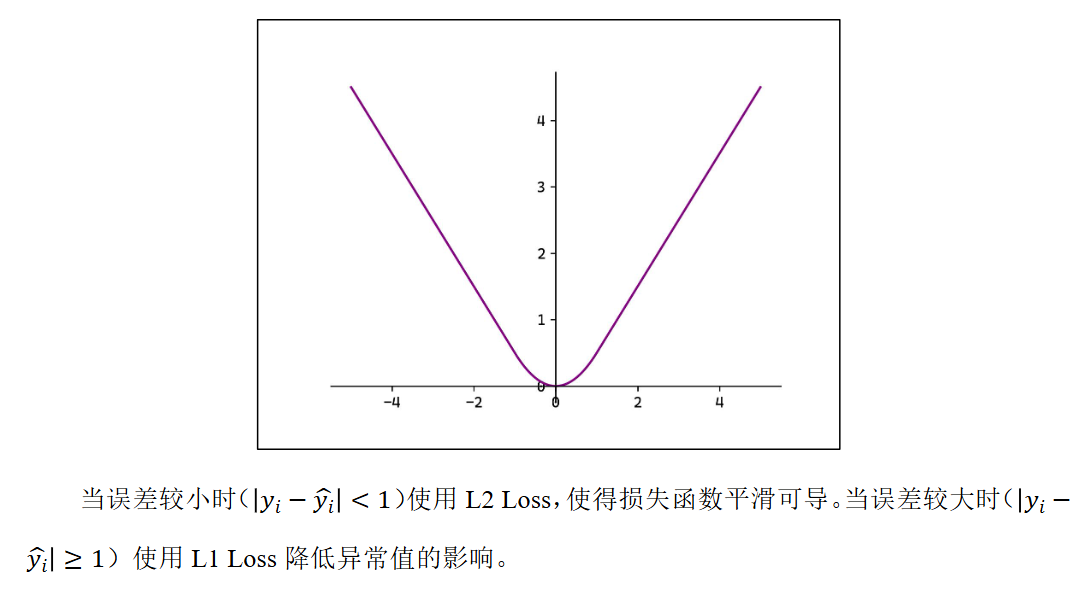
平滑 L1:
随机梯度下降法(SGD)
在神经网络的学习过程中,可以使用梯度下降法来更新参数,目标就是减小损失函数的 值。
实际操作时,一般会从训练数据中随机选择一个小批量数据(mini-batch),然后用梯 度下降法迭代多个轮次(iteration);这种“对随机选择的数据进行的梯度下降法”,被称作随机梯度下降法(stochastic gradient descent,SGD)
反向传播
激活层的反向传播
各激活函数及其导数已在上述体现
Affine 的反向传播和实现
假设一个简单的全连接神经网络,结构如下(从输入到输出):
输入层 → 全连接层(Affine)→ 激活层(如 ReLU)→ 全连接层(Affine)→ 激活层(如 Softmax)→ 输出层(损失计算)
可以大致分为这几类层:
输出层(Output Layer):通常是最后一个全连接层(Affine),后面接一个损失函数(比如交叉熵损失)
激活层(Activation Layer):非线性层(如 ReLU、Sigmoid、Softmax),负责引入非线性能力(没有可训练参数,只有梯度传递)
全连接层(Affine层):线性变换层(y=Wx+b),包含可训练参数(权重 W和偏置 b)

关于affine层中y=Wx+b中为什么要对w和x都求偏导,我的理解是:最终输出层肯定有一个损失函数,可以求出损失函数的梯度,然后根据这个损失函数的梯度去修改输出层的w和b,让输出层趋近正确标签,但是x是上层传过来的,没法直接修改。但是可以求出这个x在最后这个损失函数的梯度是多少,意思是按照这个方向趋近就可以接近正确答案,然后把这个根据x求出的梯度,传给上一层,作为上一层的y=wx+b 整体要趋近的方向(梯度)。
输出层的反向传播和实现

神经网络的参数
更新参数方法的优化
SGD 的缺点
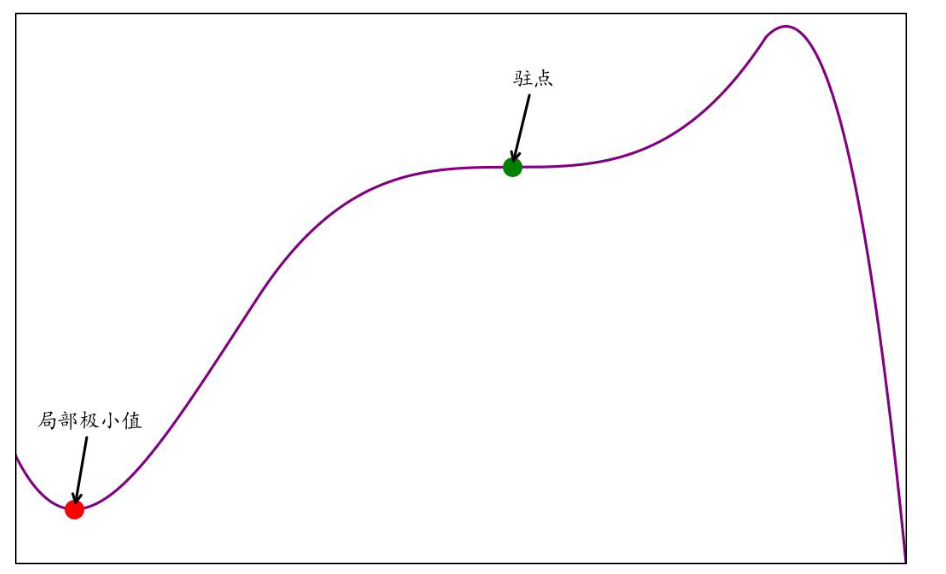
- 局部最优解:陷入局部最优,尤其在非凸函数中,难以找到全局最优解
- 鞍点:陷入鞍点,梯度为 0,导致训练停滞
- 收敛速度慢:高维或非凸函数中,收敛速度较慢
- 学习率选择:学习率过大导致震荡或不收敛,过小则收敛速度慢
Momentum
原始的梯度下降法直接使用当前梯度来更新参数:
$$
W←W−η\nabla
$$
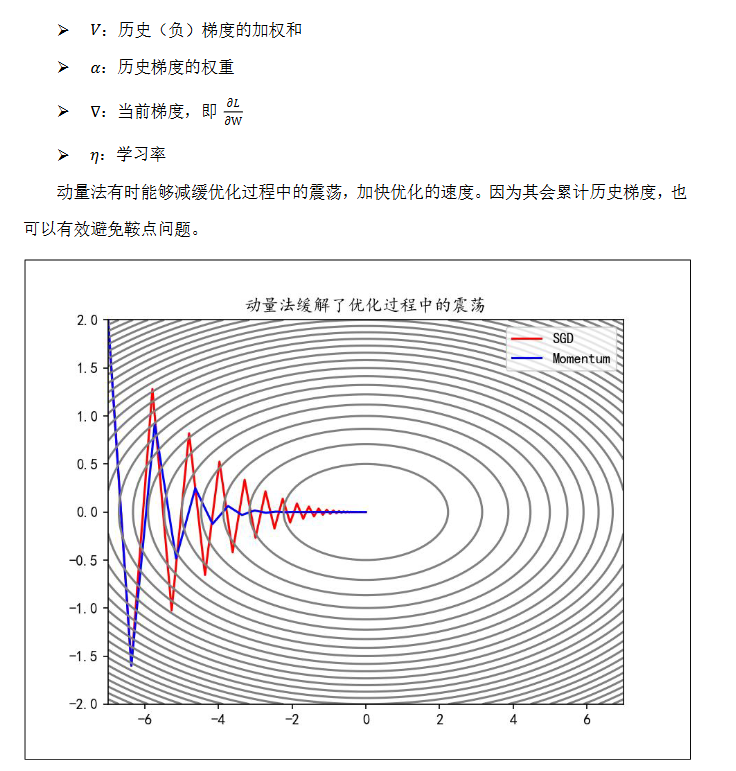
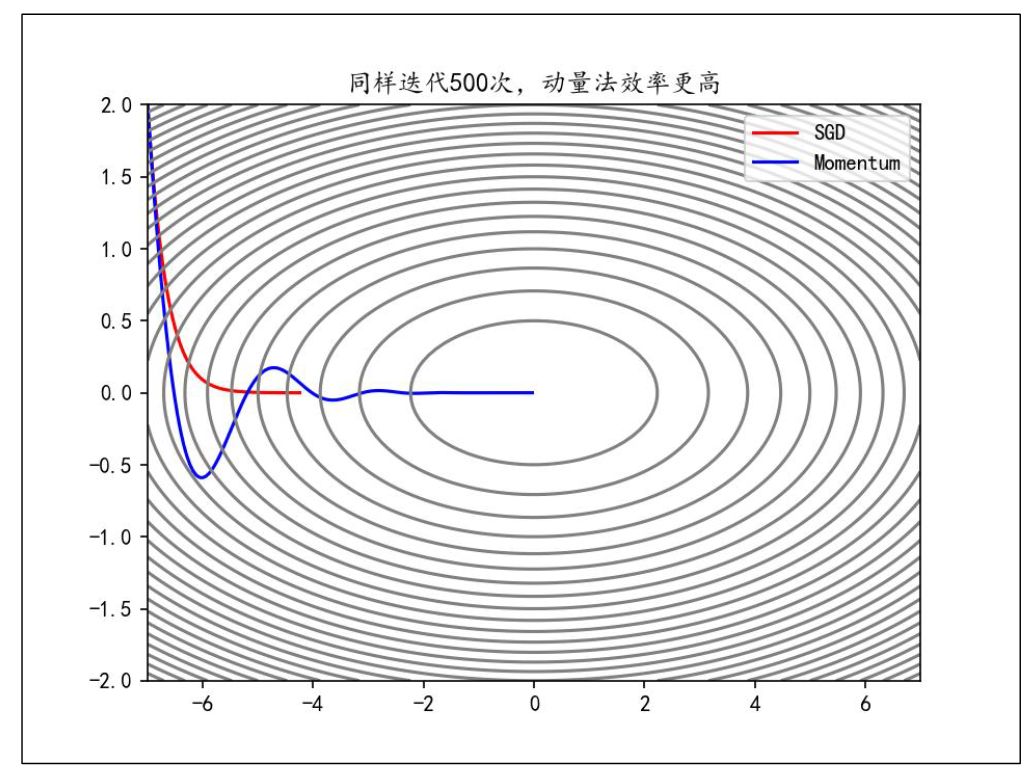
而 Momentum(动量法)会保存历史梯度并给予一定的权重,使其也参与到参数更新中:
$$
v \leftarrow \alpha v - η\nabla
$$
$$
W \leftarrow W + v
$$
学习率衰减
深度学习模型训练中调整最频繁的当属学习率,好的学习率可以使模型逐渐收敛并获得更好的精度。
较大的学习率可以加快收敛速度,但可能在最优解附近震荡或不收敛;
较小的学习率可以提高收敛的精度,但训练速度慢。
学习率衰减是一种平衡策略,初期使用较大学 习率快速接近最优解,后期逐渐减小学习率,使参数更稳定地收敛到最优解。
等间隔衰减
每隔固定的训练周期(epoch),学习率按一定的比例下降,也称为“步长衰减”。例 如,使学习率每隔 20 epoch 衰减为之前的 0.7:
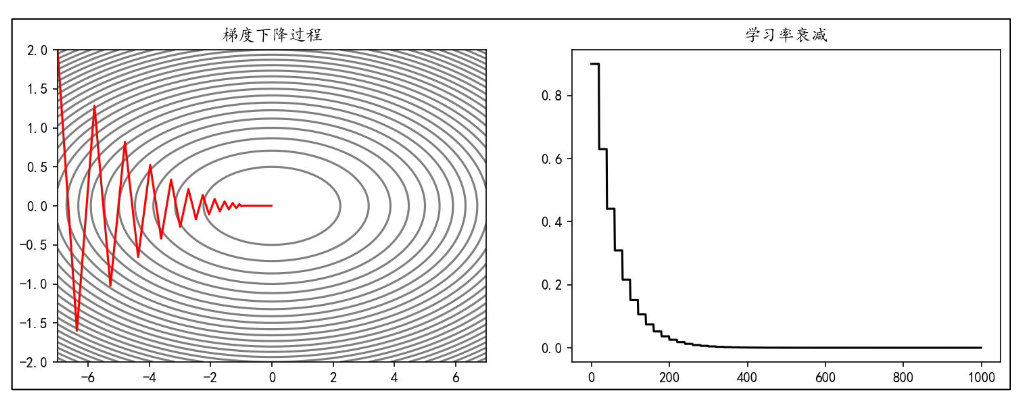
指定间隔衰减
在指定的 epoch,让学习率按照一定的系数衰减。例如,使学习率在 epoch 达到[10,50,200] 时衰减为之前的 0.7:
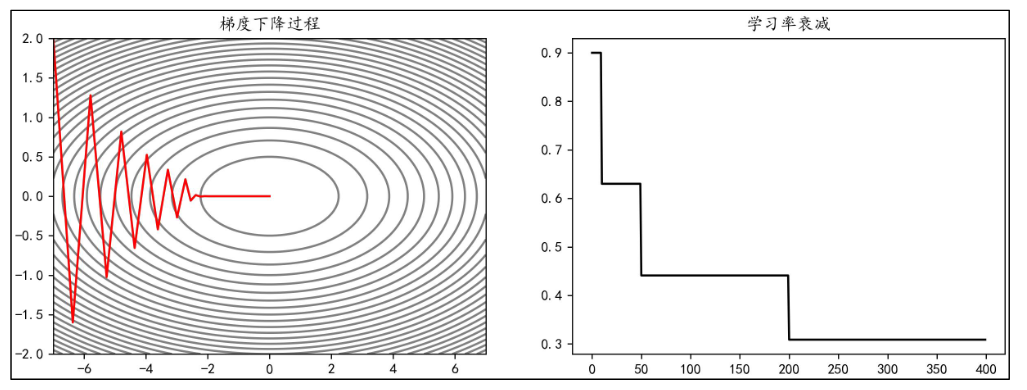
指数衰减
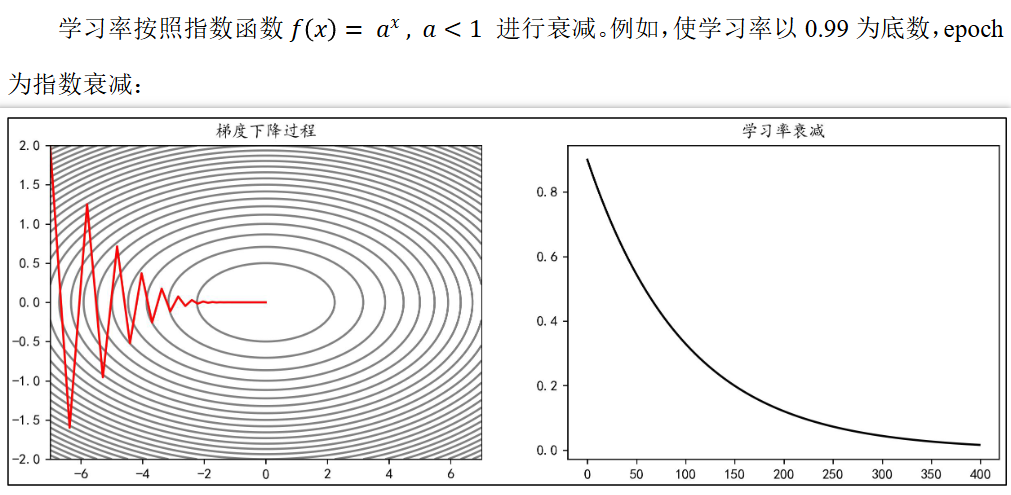
AdaGrad

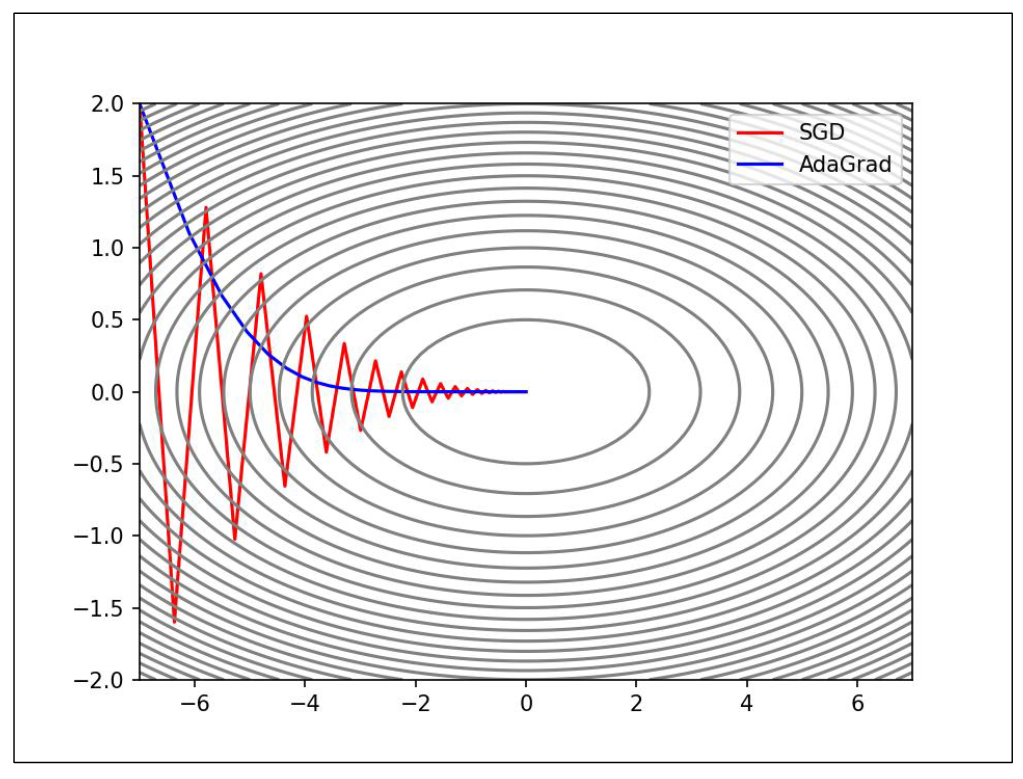
RMSProp
RMSProp(Root Mean Square Propagation,均方根传播)是在 AdaGrad 基础上的改进, 它并非将过去所有梯度一视同仁的相加,而是逐渐遗忘过去的梯度,采用指数移动加权平均, 呈指数地减小过去梯度的尺度。
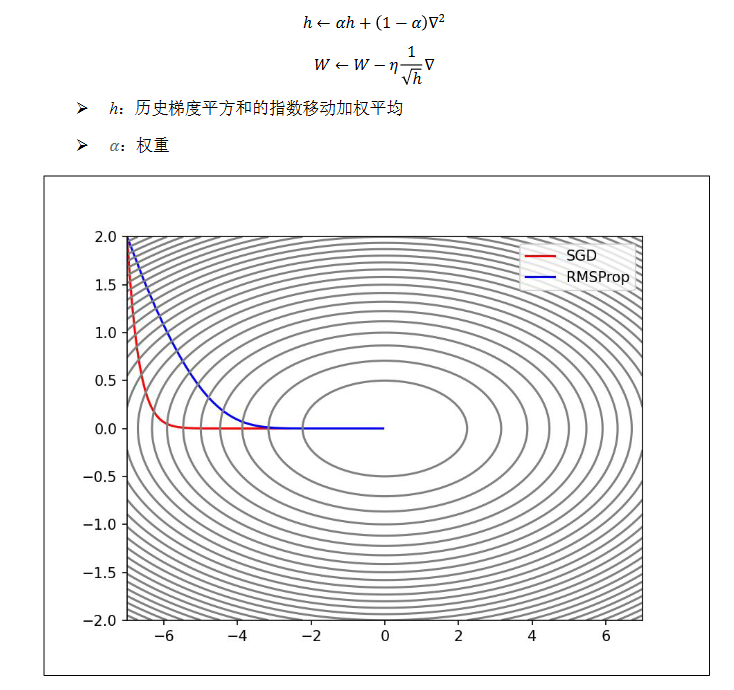
Adam
Adam(Adaptive Moment Estimation,自适应矩估计)融合了 Momentum 和 AdaGrad 的 方法。
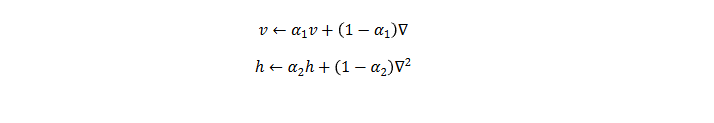
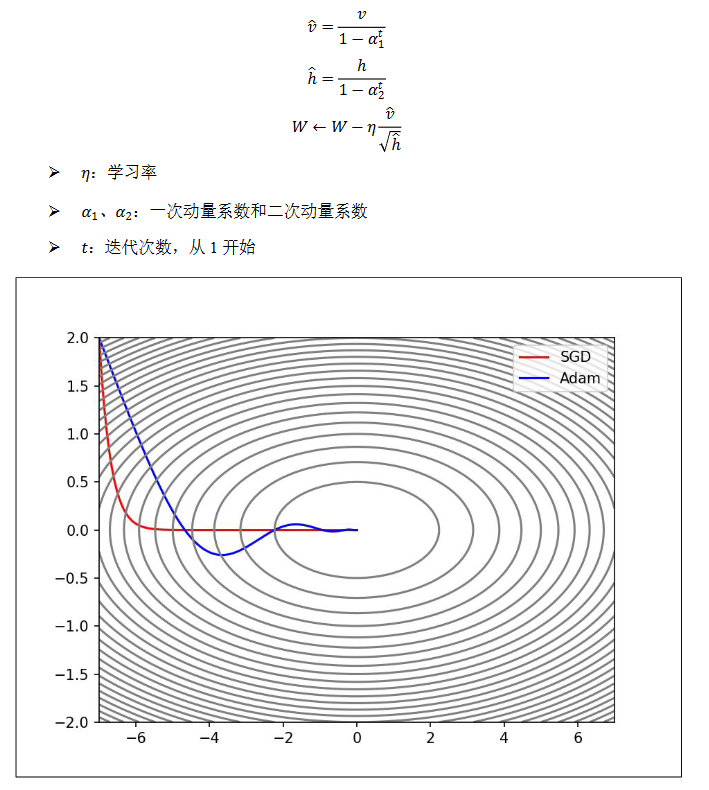
参数初始化
常数初始化
所有权重参数初始化为一个常数,即 W = k · J
这里 J 为全 1 矩阵,k 为初始化的常数。 注意:将权重初始值设为 0 将无法正确进行学习。严格地说,不能将权重初始值设成一 样的值。因为这意味着反向传播时权重全部都会进行相同的更新,被更新为相同的值(对称 的值)。这使得神经网络拥有许多不同的权重的意义丧失了。为了防止“权重均一化”(瓦 解权重的对称结构),必须随机生成初始值。
秩初始化
权重参数初始化为单位矩阵,即 W = I 这里 I 为单位矩阵,即主对角线上元素为 1,其它元素为 0。
正态分布初始化

均匀分布初始化
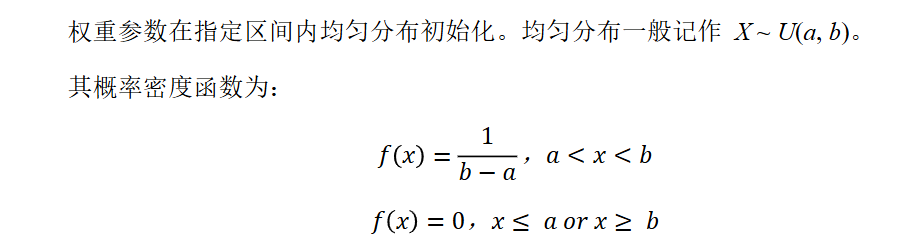
Xavier 初始化(也叫 Glorot 初始化)
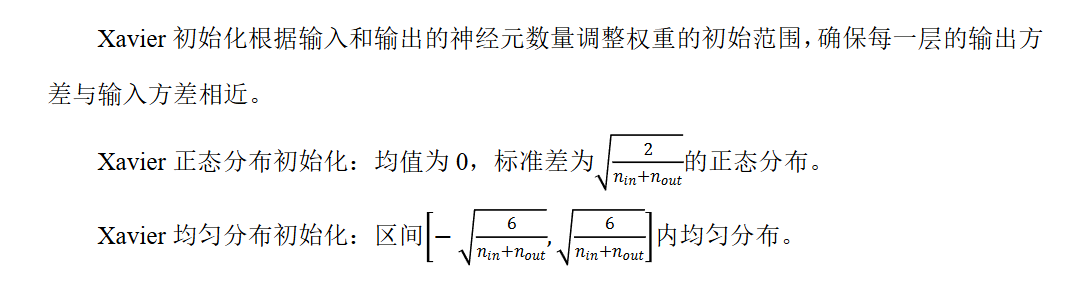

He 初始化(也叫 Kaiming 初始化)

正则化
机器学习的问题中,过拟合 是一个很常见的问题。
过拟合指的是能较好拟合训练数据,但不能很好地拟合不包含在训练数据中的其他数据。 机器学习的目标是提高泛化能力,希望即便是不包含在训练数据里的未观测数据,模型也可 以进行正确的预测。因此可以通过 正则化 方法来抑制过拟合。
常用的正则化方法有 Batch Normalization、权值衰减、Dropout、早停法等。
Batch Normalization 批量标准化
Batch Normalization 最重要的目的,其实是调整各层的激活值分布使其拥有适当的广度, BN 层通常放在线性层(全连接层/卷积层)之后,激活函数之前。它有着以下优点:
- 可以使学习快速进行(允许更高的学习率)
- 不那么依赖初始值(对于初始值不用那么神经质)
- 抑制过拟合(降低 Dropout 等的必要性)

权值衰减

Dropout 随机失活
Dropout(随机失活,暂退法)是一种在学习的过程中随机关闭神经元的方法。
训练时以概率p随机关闭神经元,迫使网络不依赖特定神经元,增强鲁棒性,同时未被 关闭的神经元的输出值以 1/1−p 的比例进行缩放,以保持期望值不变;而测试时通常不使用 Dropout,即所有神经元保持激活状态并且不进行缩放。
Dropout 会有隐式集成的效果(每次迭代训练不同的子网络,测试时近似集成效果)。
Dropout 在全连接层和卷积层均适用,尤其对大规模网络效果显著。Dropout 通常放在 激活函数之后,线性层(全连接层/卷积层)之前。
卷积神经网络
卷积神经网络(Convolutional Neural Network,CNN)常被用于图像识别、语音识别等 各种场合。它在计算机视觉领域表现尤为出色,广泛应用于图像分类、目标检测、图像分割 等任务。
卷积神经网络的灵感来自于动物视觉皮层组织的神经连接方式,单个神经元只对有限区 域内的刺激作出反应,不同神经元的感知区域相互重叠从而覆盖整个视野。
CNN 中新出现了卷积层(Convolution 层)和池化层(Pooling 层),下图是一个 CNN 的结构:
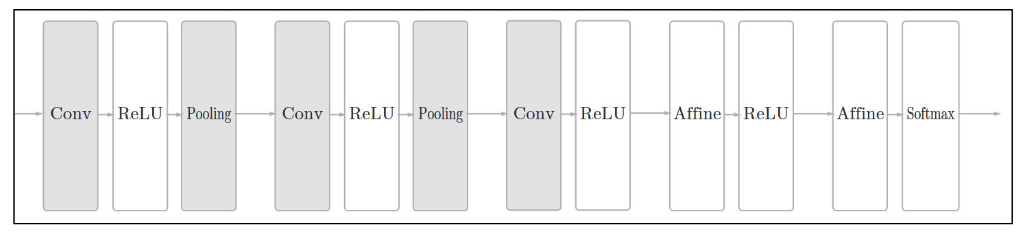
- 卷积层用于提取输入数据的局部特征。
- 池化层用于降维,增强鲁棒性并防止过拟合。
- 全连接层用于整合特征并输出结果。
卷积层
卷积运算
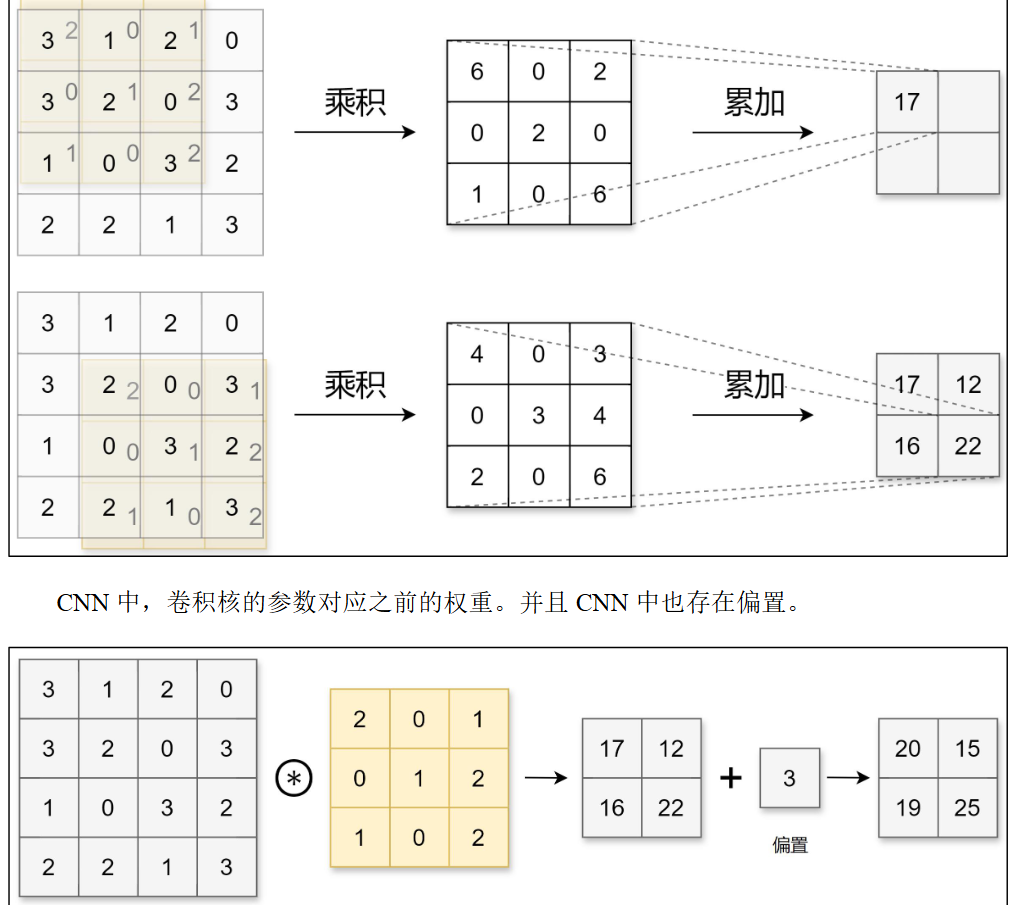
填充
在进行卷积层的处理之前,有时要向输入数据的周围填入固定的数据(比如 0),这称 为填充(padding)。例如,对形状为 4×4 的数据进行幅度为 1 的填充,即用幅度为 1、值 为 0 的数据填充周围:
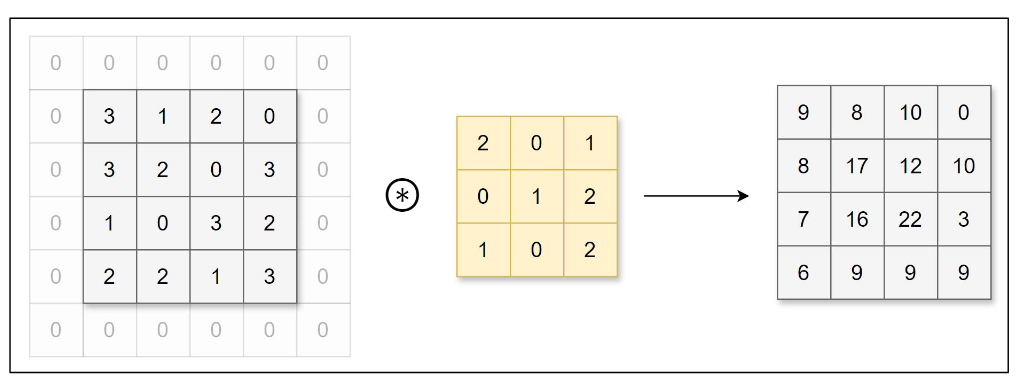
可以看到,4×4 的数据进行幅度为 1 的填充后形状变为 6×6,再经过卷积后数据的形 状为 4×4。使用填充主要目的是为了调整输出数据的形状大小,避免多次卷积后数据形状 大小过小导致无法继续进行卷积运算。运用填充可以令数据形状在经过卷积运算后保持不变。
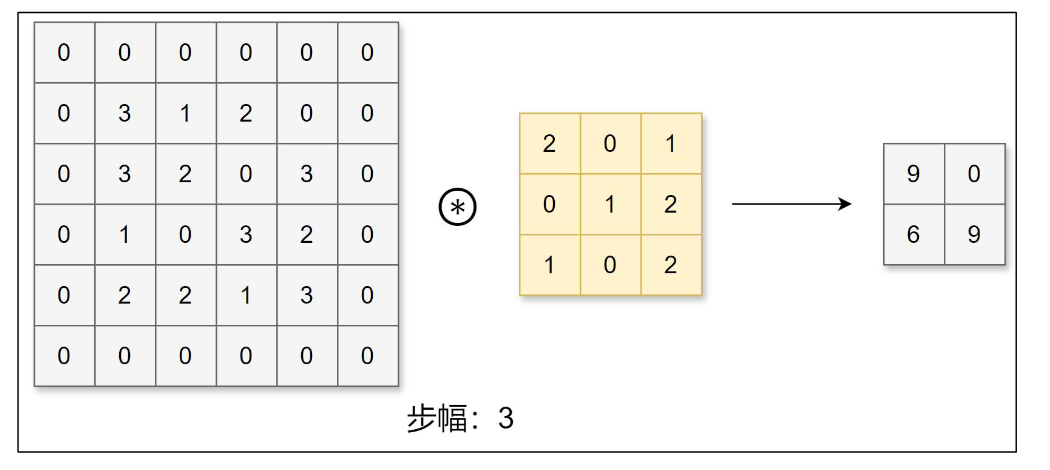
步幅
应用卷积核的位置间隔称之为步幅(stride)。
之前的例子中步幅都为 1,下面我们进行步幅为 3 的卷积运算:

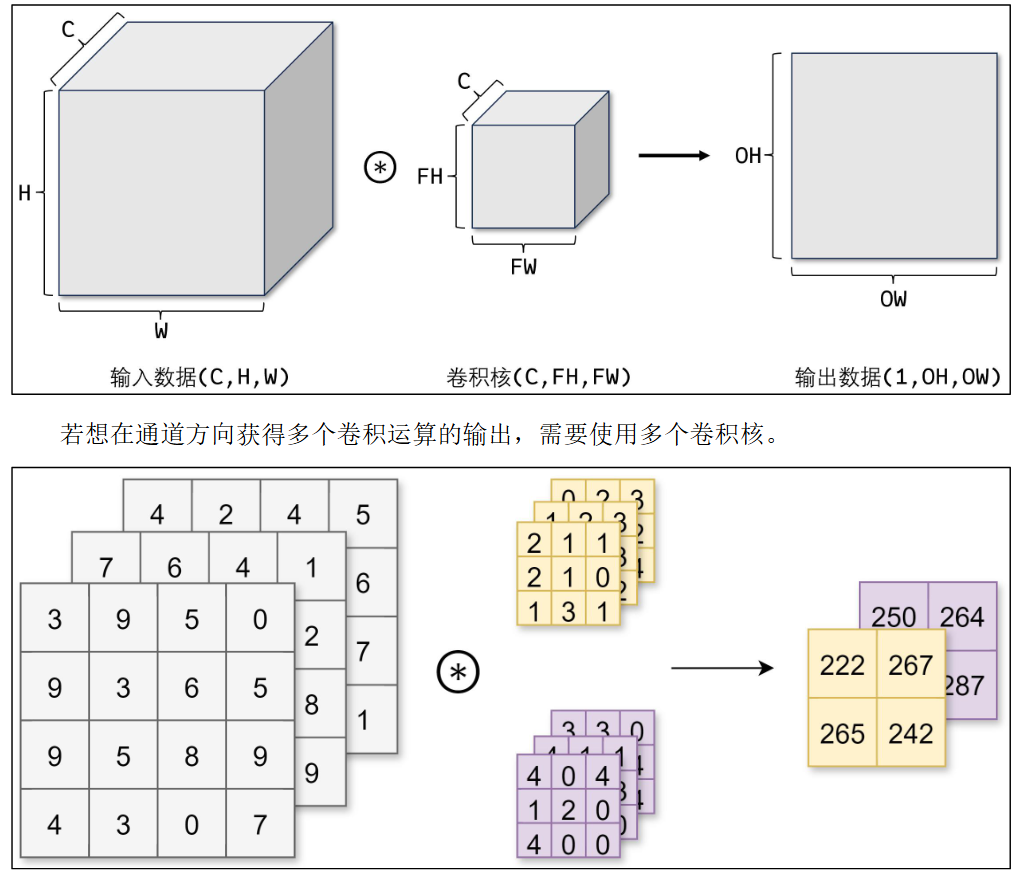
三维数据的卷积运算
图像是 3 维数据,除了长、宽外还需要处理通道方向。在 3 维数据的卷积运算中,输入 数据的通道数和卷积核的通道数须设为相同的值。当有多个通道时,会按通道进行输入数据 和卷积核的卷积运算,并将结果相加得到输出数据。
池化层
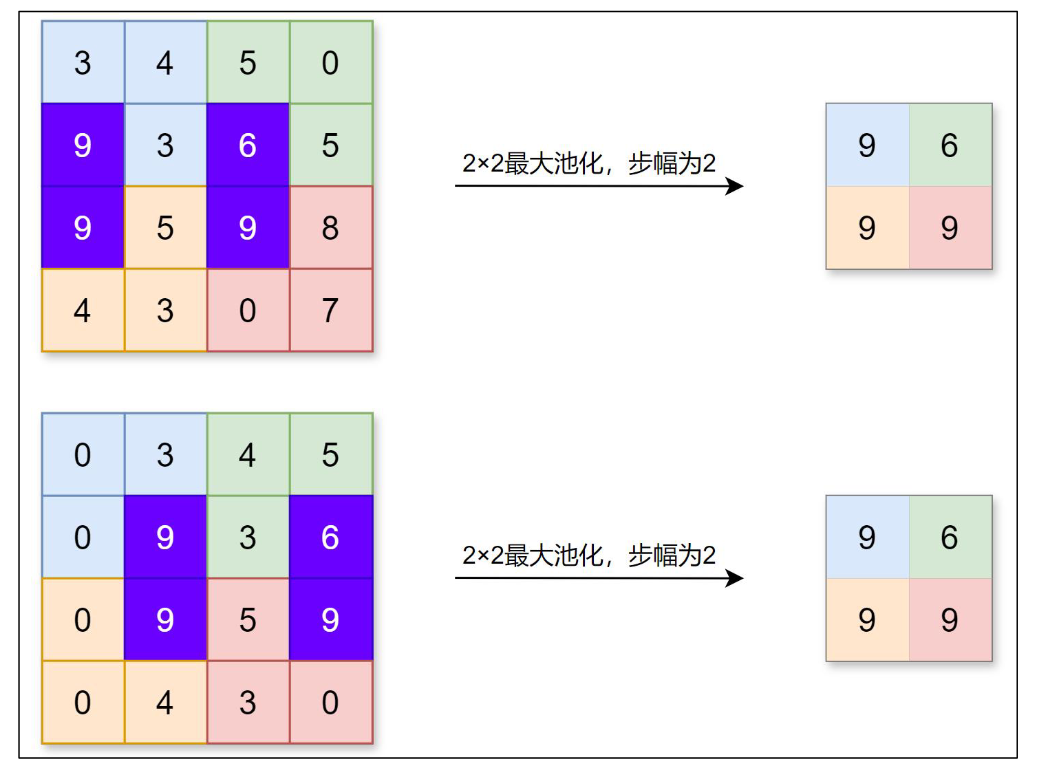
池化层缩小长、宽方向上的空间来进行降维,能够缩减模型的大小并提高计算速度。例 如,对数据进行步幅为 2 的 2×2 的 Max 池化:
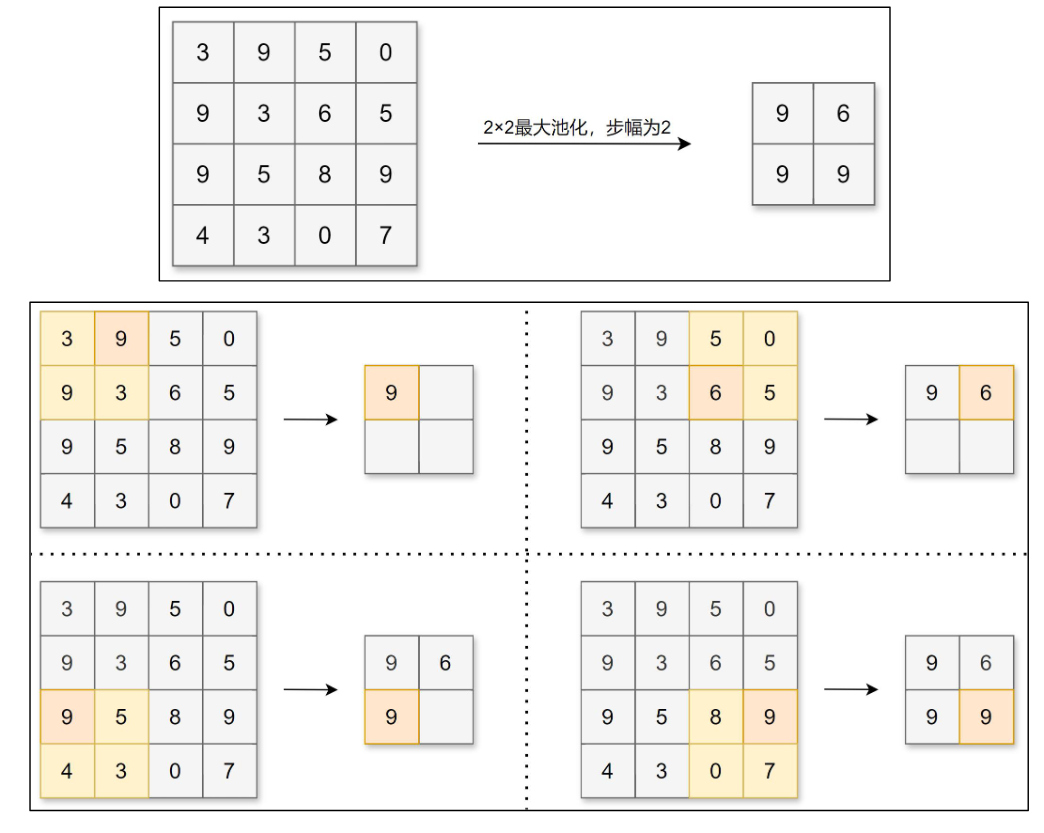
除了 Max 池化(计算窗口内的最大值),还有 Average 池化(平均池化,计算窗口内 的平均值)等。一般会将池化的大小窗口和步幅设置为相同的值,比如 2×2 的窗口大小, 步幅会设置为 2。池化同样也可以设置填充。 和卷积层不同,池化层没有要学习的参数,并且池化运算按通道独立进行,经过池化运 算后数据的通道数不会发生变化。
池化的另一个特点是对微小偏差具有鲁棒性,数据发生微小偏差时,池化可能会返回相 同的结果。例如,数据在宽度方向上偏离 1 个元素,返回的结果不变。