机器学习总结

基本理论

机器学习方法 = 模型 + 策略 + 算法

组成部分	对应问题	体现
模型	学习什么？—— 学习一个函数（或映射关系）的形式	线性回归 / 逻辑回归
策略	按什么准则去学习？—— 定义什么是“好”的模型	均方误差 / 交叉熵
算法	怎么学？—— 如何找到最优模型	梯度下降 / 随机梯度下降 / 反向传播

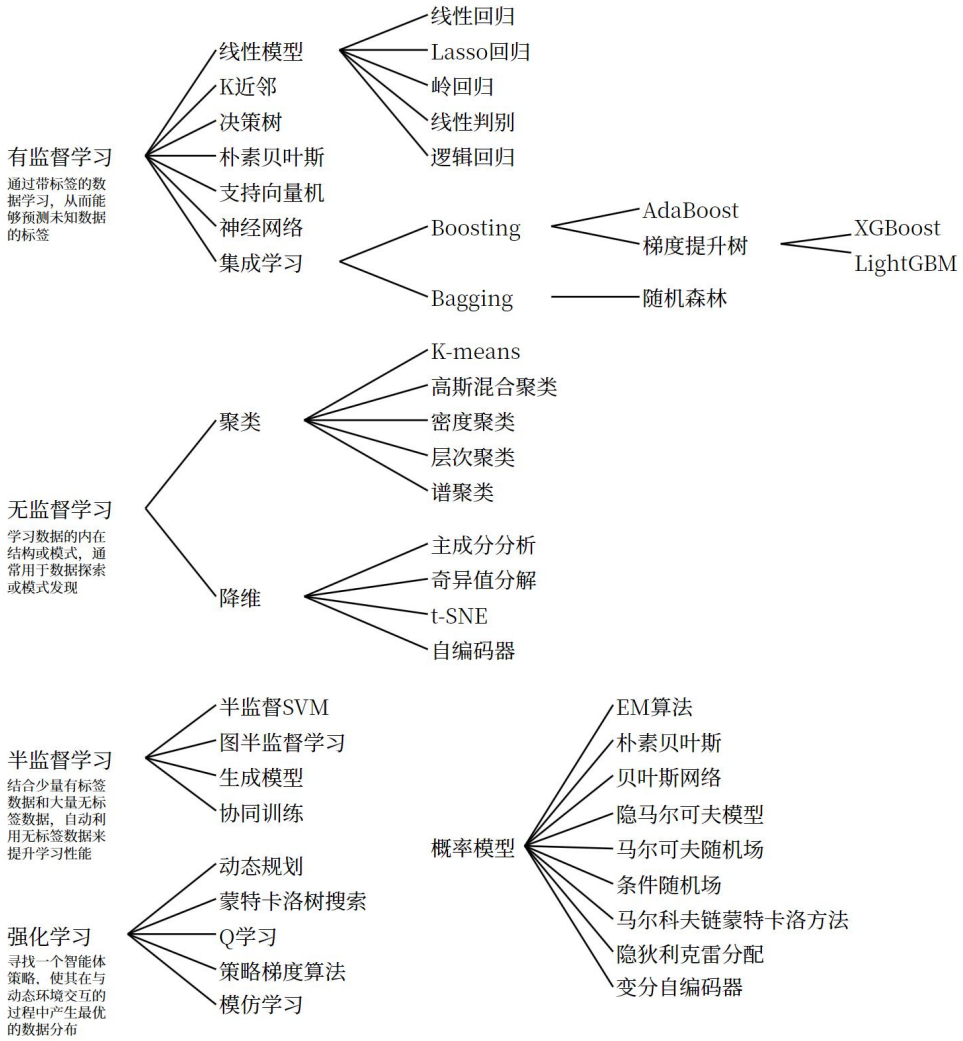
机器学习主要分类

有监督学习：提供数据并提供数据对应结果的机器学习过程。
无监督学习：提供数据并且不提供数据对应结果的机器学习过程。
半监督学习：提供一部分数据有标签，另一部分数据没有标签，同时利用有标签和无标签的数据进行学习。
强化学习：模型通过与环境的交互，根据采取的行动获得奖励信号，目标是学会采取一系列行动以最大化长期累积奖励。

特征工程

特征选择

特征选择不会创建新特征，也不会改变数据结构。

方法类型	核心思想	实现
(1) 过滤法 (Filter Method)	基于特征与目标变量的统计相关性进行筛选，独立于模型训练过程。	对于数值型目标 → 皮尔逊相关系数、方差分析（ANOVA）对于类别型目标 → 卡方检验、互信息（Mutual Information）
(2) 包裹法 (Wrapper Method)	通过模型性能评估不同特征子集的效果，选择使模型表现最优的特征组合。	递归特征消除（基于模型权重）前向选择（逐步添加最优特征）后向消除（逐步剔除最差特征）
(3) 嵌入法 (Embedded Method)	模型在训练过程中自动学习特征重要性，并基于学习到的特征权重或贡献度进行筛选。	Lasso 回归（L1 正则化，系数压缩）树模型（如 XGBoost、LightGBM，基于特征重要性）

特征转换

归一化（Normalization）

将数据按比例缩放到一个固定范围[min, max]（通常是[0, 1]或[ − 1, 1]）。

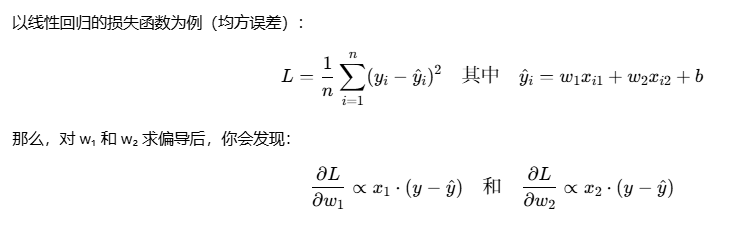
标准化（Standardization）

将数据调整为均值为 0、标准差为 1 的标准分布。

共同目的：归一化和标准化都是数据预处理方法，目的是 让不同特征具有可比性，提升模型训练效果和收敛速度。通过对原始数据进行变换，避免某些特征因数值范围过大或过小而对模型产生不合理的影响，使模型更加稳定、高效。
具体目的
- 消除量纲影响：不同特征可能具有不同的单位和量级，如身高（厘米）和体重（千克），直接使用原始数据会使数值大的特征在模型中占据主导地位，归一化和标准化可以解决这一问题。
- 加快模型收敛：在机器学习算法中，尤其是基于梯度下降的算法（如神经网络、逻辑回归），数据的尺度会影响梯度的更新速度。经过归一化或标准化处理后，数据分布更均匀，模型能够更快地收敛到最优解。
- 提高模型性能：合适的数据预处理可以使模型更好地学习数据中的模式和规律，从而提高模型的准确性、稳定性和泛化能力。

对数变换

对于有偏态的分布（如收入、价格、点击量等），对数变换可以将其转化为更接近正态分布的形式。

例：比如“用户观看次数”字段中，大多数人看了 1~10 次，但少数人看了 1000 次。直接用原始数据，模型可能会被极少数高观看用户主导。对观看次数字段做对数变换后，分布会更平滑、合理，模型效果通常会更好。

对数变换主要用于处理“右偏、长尾、有极端大值”的数据，将大数值压缩，小数值相对放大，从而减小极端值的影响力，使整体分布更平滑、更对称，更接近正态分布减少极端值对模型的影响。

而标准化主要用于统一数据的尺度和范围，让不同特征具有可比性，但不会改变原始数据的分布形状或压缩极端值。因此，在面对像“用户观看次数”这种少数人极高的情况时，对数变换通常是更合适的选择。

类别变量的编码

独热编码（One-Hot Encoding）：将类别型变量转换为二进制列，常用于无序类别特征。
标签编码（Label Encoding）：将类别型变量映射为整数，常用于有序类别特征。
目标编码（Target Encoding）：将类别变量的每个类别替换为其对应目标变量的平均值或其他统计量。每个类别本身可能没有直观的数值意义，但如果我们知道属于该类别的样本，其目标值（比如房价）的平均值是多少，就可以用这个平均值来代表该类别

每个类别本身可能没有直观的数值意义，但如果我们知道 属于该类别的样本，其目标值（比如房价）的平均值是多少，就可以用这个平均值来代表该类别

这种方法能捕捉类别与目标之间的关系，通常比独热编码或标签编码更有信息量
频率编码（Frequency Encoding）：将类别变量的每个类别替换为该类别在数据集中的出现频率。

特征构造

交互特征：将两个特征组合起来，形成新的特征

例如，将年龄与收入结合创建新的特征，可能能更好地反映某些模式。
统计特征：从原始特征中提取统计值，例如求某个时间窗口的平均值、最大值、最小值、标准差等。
日期和时间特征：从日期时间数据中提取如星期几、月份、年份、季度等特征。

特征降维

主成分分析（PCA）：当你的数据维度太高（比如几百个特征），但很多特征可能是冗余或相关的
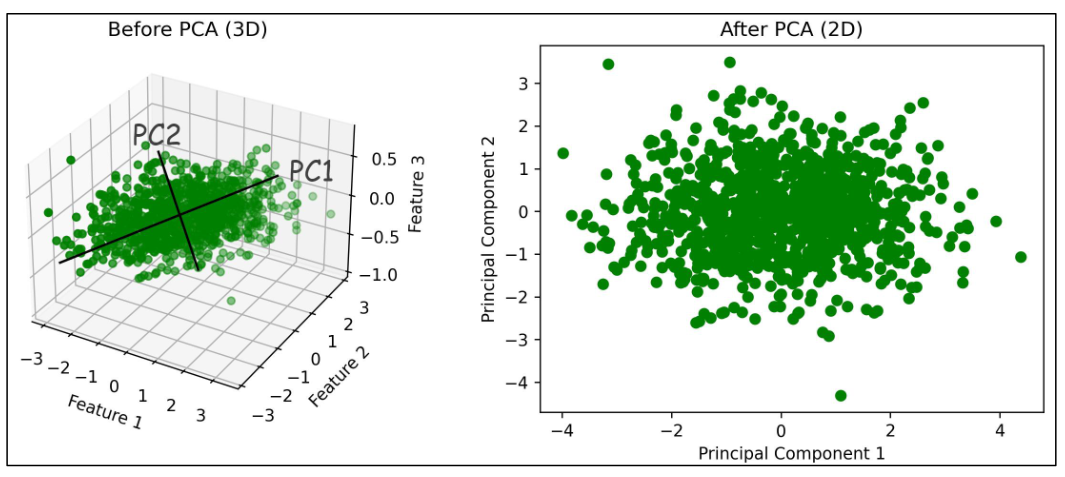
线性判别分析（LDA）：不是单纯地保留数据方差（像 PCA），而是最大化类别之间的分离度，最小化类别内部的散度

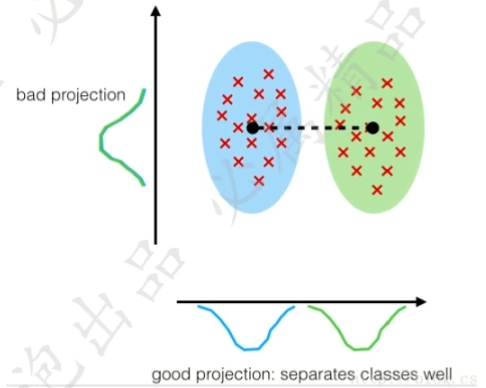
对比项	PCA（主成分分析）	LDA（线性判别分析）
监督性	❌ 无监督	✅ 有监督（需要类别标签）
目标	最大化数据方差（保留信息）	最大化类间距离，最小化类内散度（优化分类）
是否使用标签	不使用	使用
适用场景	降维、去噪、可视化	分类任务中的降维、特征提取
投影方向	数据方差最大的方向	类间分离度最大的方向

奇异值分解（Singular Value Decomposition，简称 SVD）

把一个复杂的数据矩阵（比如用户对电影的评分表），拆解成几个简单的“组件”：

一些代表用户偏好的方向（U）

一些代表它们之间关联强度的数字（Σ，奇异值，越大越重要）

一些代表物品（如电影）特征的方向（V）

奇异值分解（SVD）是一种强大的矩阵分解技术，用于发现数据中的主要结构与重要信息，可以实现数据降维、压缩和模式提取，广泛应用于推荐系统、图像处理等领域；

而 PCA 是一种基于方差最大化的降维方法，通常通过 SVD 实现，专注于保留数据中的最大变化方向。两者有紧密联系，但 SVD 更通用，PCA 更专注于统计意义上的降维与可视化。

模型评估和模型选择

损失函数

0-1 损失函数（Zero-One Loss）

用于分类任务，判断预测结果是否正确：

$$
L(Y, f(X)) =
\begin{cases}
1, & Y \neq f(X) \
0, & Y = f(X)
\end{cases}
$$

说明：若预测值 f(X) 与真实标签 Y 不相等，损失为 1；否则为 0。
特点：非连续、非凸，一般不直接用于优化，但概念重要。

平方损失函数（Square Loss / L2 Loss）

常用于回归问题，衡量预测值与真实值的平方差：

$$
L(Y, f(X)) = (Y - f(X))^2
$$

说明：预测值与真实值之差的平方，越小表示预测越准。
特点：连续可导，常用于线性回归等模型。

绝对损失函数（Absolute Loss / L1 Loss）

也用于回归问题，衡量预测值与真实值的绝对差：

$$
L(Y, f(X)) = |Y - f(X)|
$$

说明：预测值与真实值之差的绝对值，对异常值比平方损失更鲁棒。
特点：不可导在零点，但对离群点更稳健。

对数似然损失函数（Log-Likelihood Loss / Negative Log Likelihood）

常用于分类问题，尤其是输出概率的场景（如逻辑回归）：

$$
L(Y, P(Y|X)) = -\log P(Y|X)
$$

说明：衡量模型预测的概率分布 P(Y|X) 与真实标签 Y 之间的差异，越小表示预测概率越接近真实。
特点：常用于逻辑回归、神经网络分类等输出概率的模型。
注意：这里的 P(Y|X) 是模型预测的“给定 X 下 Y 的概率”。

经验误差

给定一个训练数据集，数据个数为 n：

$$
T = {(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)}
$$

根据选取的损失函数，就可以计算出模型 f(X) 在训练集上的平均误差，称为训练误差，也被称作：

经验误差（empirical error）
经验风险（empirical risk）

数学表达式为：

$$
R_{\text{emp}}(f) = \frac{1}{n}\sum_{i=1}^{n} L(y_i, f(x_i))
$$

类似地，在测试数据集上的平均误差，被称为：

测试误差
或 泛化误差（generalization error）

一般情况下对模型评估的策略，就是考察经验误差；当经验风险最小时，就认为取到了最优的模型。这种策略被称为 经验风险最小化（empirical risk minimization，ERM）。

欠拟合与过拟合

欠拟合（Underfitting）：是指模型在训练数据上表现不佳，无法很好地捕捉数据中的规律。这样的模型不仅在训练集上表现不好，在测试集上也同样表现差。
过拟合（Overfitting）：是指模型在训练数据上表现得很好，但在测试数据或新数据上表现较差的情况。过拟合的模型对训练数据中的噪声或细节过度敏感，把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质，从而失去了泛化能力。

正则化

正则化（Regularization）是一种在训练机器学习模型时，在损失函数中添加额外项，来惩罚过大的参数，进而限制模型复杂度、避免过拟合，提高模型泛化能力的技术。

L1 正则化（Lasso 回归）

$$
Loss_{L1}=\text {原Loss}+\lambda\sum_{i=1}^{k}\left|\omega_{i}\right|
$$

特点：L1 正则化会使一些不重要的参数变为零，从而起到特征选择的作用。它倾向于产生稀疏的权重向量，也就是很多特征的系数会变成 0，这样就可以筛选出对模型预测最有价值的特征，常用于特征数量较多且存在大量无关特征的场景。
$$
\text{总损失} = |1 - \omega| + \lambda \cdot |\omega| = |1 - \omega| + |\omega|
$$

应用场景：适用于特征选择、数据维度较高的情况，比如在文本分类任务中，从大量的文本特征中筛选出重要的特征。

L2 正则化（Ridge 回归，岭回归)

$$
Loss_{L2} = \text{原Loss} + \lambda \sum_{i=1}^{k} \omega_i^2
$$

特点：L2 正则化不会让参数变为零，而是让每个参数的值都变小，使得模型的权重更加平滑，避免模型对某些特征过度依赖。它通过对较大的参数进行更大的惩罚，使得模型的参数不会过大，从而减少模型的复杂度，提高模型的泛化能力。
应用场景：常用于处理特征之间存在共线性的情况，比如在房价预测中，房屋面积、房间数量等特征之间可能存在一定的相关性，使用 L2 正则化可以让模型更加稳定。

ElasticNet 正则化(弹性网络回归)

$$
Loss_{ElasticNet} = \text{原Loss} + \lambda \left( \alpha \sum_{i=1}^{n} \left| \omega_i \right| + \frac{1 - \alpha}{2} \sum_{i=1}^{n} \omega_i^2 \right)
$$

特点：当 α接近 1 时，ElasticNet 更接近 L1 正则化，具有特征选择的能力；当 α接近 0 时，ElasticNet 更接近 L2 正则化，能让参数更加平滑。它既可以像 L1 正则化一样进行特征选择，又可以像 L2 正则化一样让参数更加平滑，综合了两者的优势。
应用场景：适用于特征数量较多且特征之间存在相关性的情况，比如在生物信息学中，分析基因表达数据时，既需要筛选出重要的基因特征，又要避免模型过拟合，ElasticNet 就是一个不错的选择。

交叉验证

交叉验证（Cross-Validation）是一种评估模型泛化能力的方法，通过将数据集划分为多个子集，反复进行训练和验证，以减少因单次数据划分带来的随机性误差。通过交叉验证能更可靠地估计模型在未知数据上的表现。亦能避免因单次数据划分不合理导致的模型过拟合或欠拟合。

简单交叉验证（Hold-Out Validation）

将数据划分为训练集和验证集（如 70%训练，30%验证）。结果受单次划分影响较大，可能高估或低估模型性能。

k 折交叉验证（k-Fold Cross-Validation）

将数据均匀分为 k 个子集（称为“折”），每次用 k−1 折训练，剩余 1 折验证，重复 k 次后取平均性能。充分利用数据，结果更稳定。

留一交叉验证（Leave-One-Out，LOO）

每次仅留一个样本作为验证集，其余全部用于训练，重复直到所有样本都被验证一次。适用于小数据集，计算成本极高。

模型评价指标

回归模型评价指标

平均绝对误差（MAE）

$$
MAE = \frac{1}{n}\sum_{i=1}^{n}|f(x_i) - y_i|
$$

MAE 对异常值不敏感，解释直观。适用于数据包含异常值的场景。

均方误差（MSE）

$$
MSE = \frac{1}{n}\sum_{i=1}^{n}\left(f\left(x_{i}\right) - y_{i}\right)^{2}
$$

MSE 会放大较大误差，对异常值敏感。适用于需要惩罚大误差的场景。

均方根误差（RMSE）

$$
RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}\left(f\left(x_{i}\right) - y_{i}\right)^{2}}
$$

与 MSE 类似，但量纲与目标变量一致。适用于需要直观误差量纲的场景。如果一味地试图降低 RMSE，可能会导致模型对异常值也拟合度也很高，容易过拟合。

R²（决定系数）

$$
R^{2} = 1 - \frac{\sum_{i=1}^{n}\left(f\left(x_{i}\right) - y_{i}\right)^{2}}{\sum_{i=1}^{n}\left(y_{i} - \bar{y}\right)^{2}}
$$

衡量模型对目标变量的解释能力，越接近 1 越好，对异常值敏感。

指标	适用场景	推荐使用时机
MAE	数据中存在较多异常值、离群点；希望评估“平均误差”	偏向实际业务解释，关注稳健性，如房价、医疗等领域
MSE	模型训练、参数优化；希望放大误差以强化惩罚	模型训练阶段，尤其是使用梯度下降优化时（如线性回归、神经网络）
RMSE	综合评估模型预测精度；希望误差单位与原始数据一致	回归任务中常用的综合性能指标，适合报告和对比模型
R²	模型拟合优度评价；希望判断模型解释方差的能力	模型对比、论文分析、模型整体效果评估

分类模型评价指标

混淆矩阵

准确率（Accuracy）

精确率（Precision）

召回率（Recall）

F1 分数（F1 Score）

ROC 曲线

AUC 值

常见距离度量方法

欧氏距离

欧几里得距离（Euclidean Distance）是指连接两点的线段的长度。

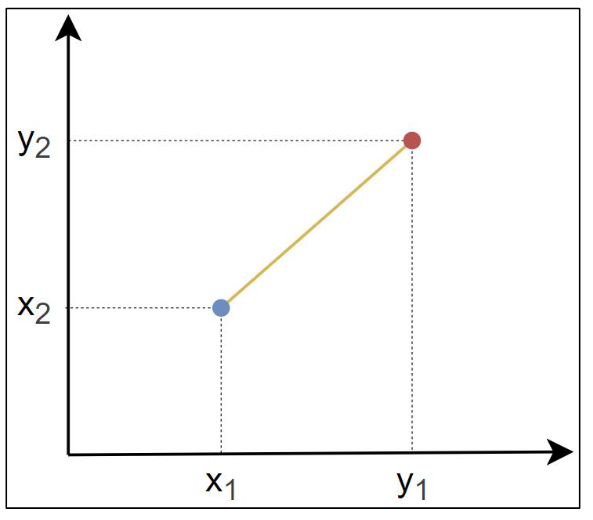
$$
d(x, y) = \sqrt{\sum_{i=1}^{n}(x_{i} - y_{i})^{2}}
$$

曼哈顿距离

曼哈顿距离（Manhattan Distance）是两点在标准坐标系上的绝对轴距之和。

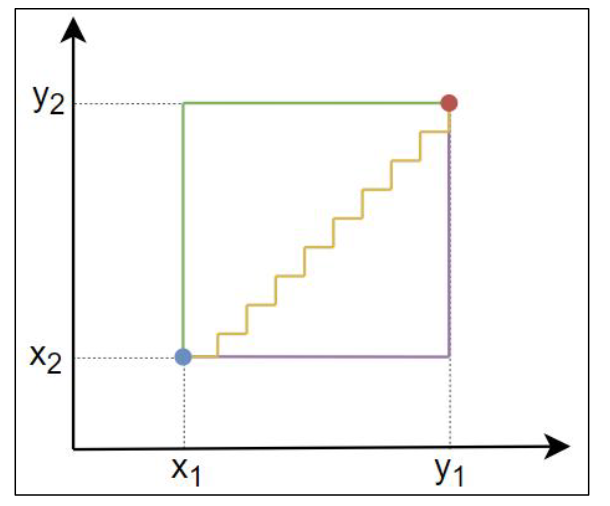
切比雪夫距离

切比雪夫距离（Chebyshev Distance）是两点各坐标数值差的最大值。

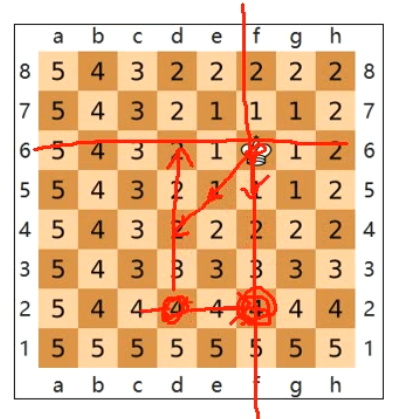
闵可夫斯基距离

线性回归

一元线性回归，多元线性回归

损失函数

均方误差（MSE）
$$
MSE = \frac{1}{n}\sum_{i=1}^{n}\left(f\left(x_{i}\right)-y_{i}\right)^{2}
$$
平均绝对误差（MAE）
$$
MAE = \frac{1}{n}\sum_{i=1}^{n}|f(x_i) - y_i|
$$

梯度下降法

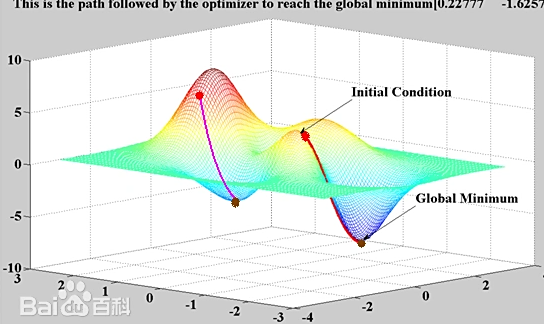
逻辑回归

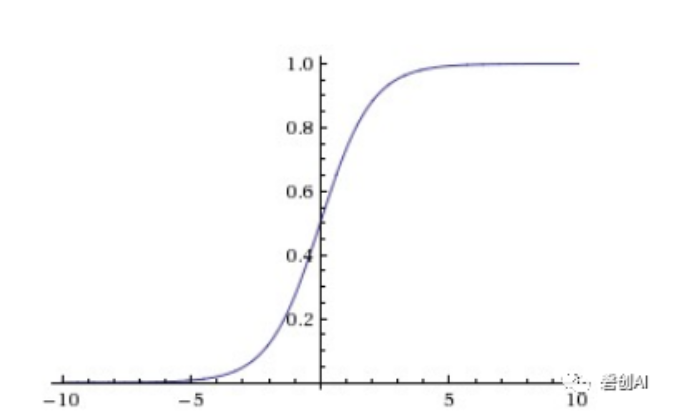
逻辑回归通过将线性回归的输出映射到[0,1]区间，来表示某个类别的概率。常用的映射函数是 sigmoid 函数：
$$
f(x) = \frac{1}{1 + e^{-x}}
$$

$$
f’(x) = f(x)(1 - f(x))
$$

逻辑回归损失函数

逻辑回归的损失函数通常使用对数损失（Log Loss），也称为二元交叉熵损失（Binary Cross-Entropy Loss），用于衡量模型输出的概率分布与真实标签之间的差距。逻辑回归的损失函数来源于最大似然估计（MLE）。

$$
Loss = -\frac{1}{n}\log L(\beta)
=-\frac{1}{n}\sum_{i=1}^{n} \left( y_i\log(P(y_i=1|x_i;\beta)) + (1-y_i)\log(1-P(y_i=1|x_i;\beta)) \right)
$$
拟合的过程就是求解似然函数的最大值，为了方便优化，令损失函数等于上述公式后来求解损失函数的最小值。

损失函数的梯度

$$
\frac{1}{n} X^T \left( \frac{1}{1 + e^{-X\beta}} - y \right)
$$

多分类任务

逻辑回归通常用于二分类问题，但可以通过一对多（One-vs-Rest，OvR）以及 Softmax 回归（Multinomial Logistic Regression，多项逻辑回归）来扩展到多分类任务。

无监督学习

聚类

K 均值聚类

K 均值聚类（K-means）是基于样本集合划分的聚类方法，将样本集合划分为k个子集构成k个簇，将n个样本分到k个簇中，每个样本到其所属簇的中心的距离最小。每个样本只能属于一个簇，所以 K 均值聚类是硬聚类。

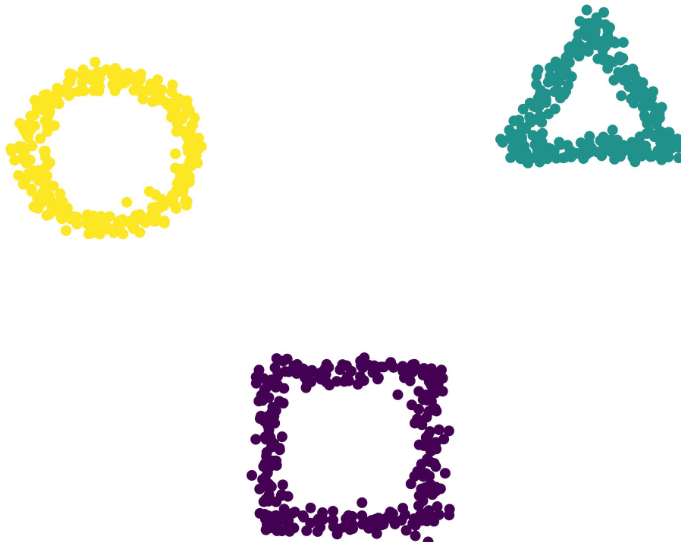
层次聚类

层次聚类（Hierarchical Clustering）假设簇之间存在层次结构，将样本聚到层次化的簇中。层次聚类有自下而上的聚合方法和自上而下的分裂方法。因为每个样本只属于一个簇，所以层次聚类属于硬聚类。

聚合聚类：开始将每个样本各自分到一个簇，之后将相距最近的两个簇合并，如此往复直至满足停止条件（例如达到预设的簇的个数、每个簇只包含一个样本、簇内样本相似性达到某个阈值等）。

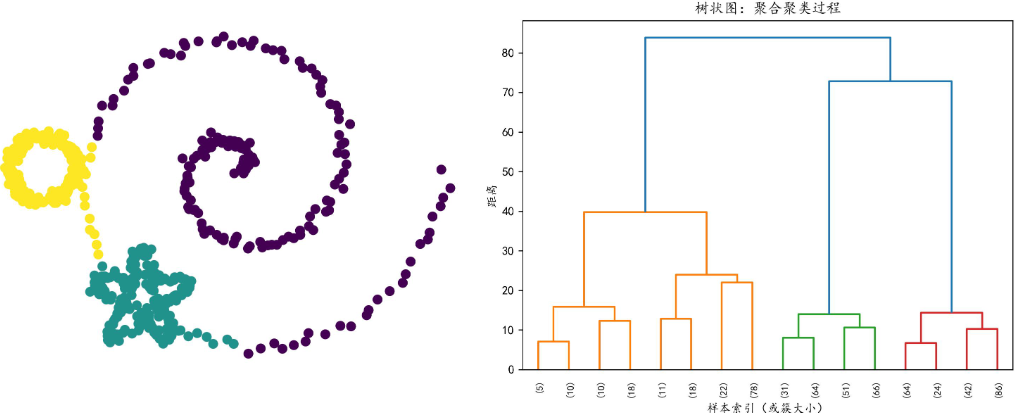
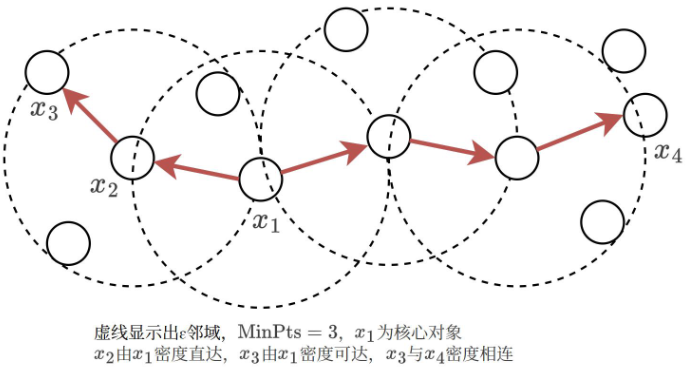
密度聚类

密度聚类（Density-Based Clustering）假设聚类结构能通过样本分布的紧密程度确定。通常情况下，密度聚类算法从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展簇以获得最终聚类效果。

聚类模型评估

轮廓系数（Silhouette Coefficient）

计算每个样本到同簇其他样本的平均距离（内聚度）和到最近其他簇样本的平均距离（分离度），综合评价聚类紧密度和分离度。

簇内平方和（Within-Cluster Sum of Squares）

衡量簇内数据点到簇中心的总距离平方和，常用于 K-means。

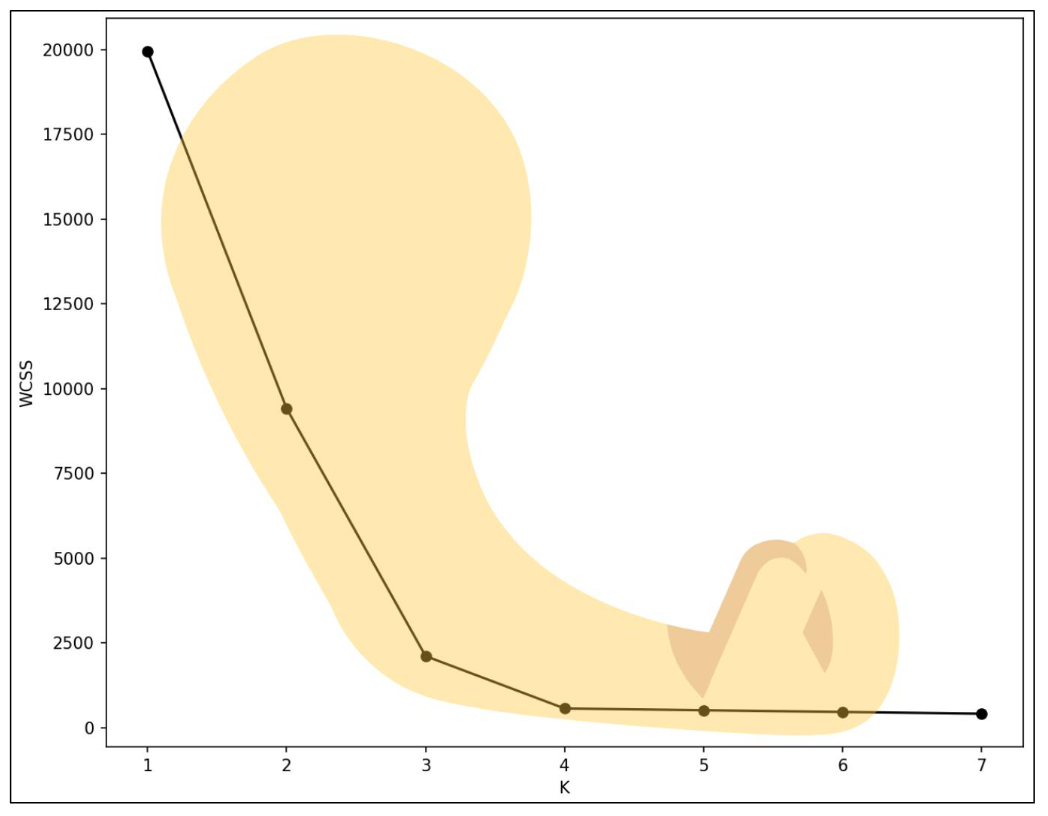
肘部法

肘部法用于确定最佳簇数K，在使用 K-means 时非常常见，它通过绘制簇数𝐀和某个聚类质量指标（通常是簇内平方和）的关系曲线，找到一个拐点或“肘部”，即增加簇数带来的收益显著减少的点，这个点通常被认为是最佳的K值。

CH 指数（Calinski-Harabasz Index）

簇间和簇内分散度的比值，也称方差比准则

其他监督学习算法

决策树

决策树（Decision Tree）是一种基于树形结构的算法，根据一系列条件判断逐步划分数据，缩小范围，最终得出预测结果。决策树由 4 部分组成：

根节点：树的节点，包含所有数据。
内部节点：表示特征上的判断条件。
分支：根据判断条件分出的路径。
叶节点：最终分类或回归的结果。

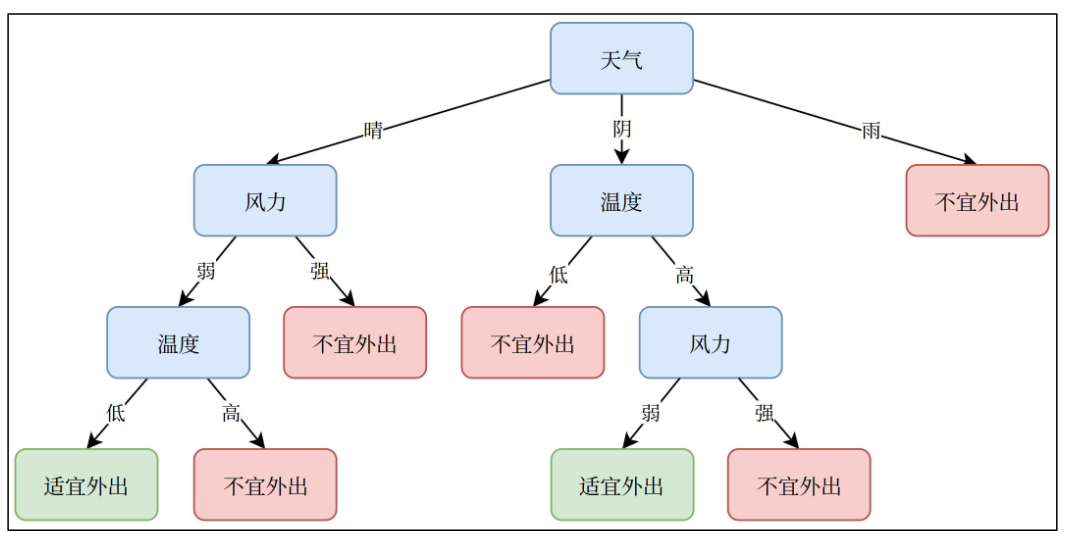
决策树工作过程

决策树的学习通常包括 3 个步骤：特征选择、决策树的生成和决策树的剪枝。

如果特征数量很多，可以在决策树学习之前对特征进行选择，只留下对训练数据有足够分类能力的特征。

决策树的生成是递归地选择最优特征，并根据该特征对训练数据进行划分，使得每个子集在当前条件下获得尽可能好的分类效果。首先构建根节点，将所有训练数据放入其中；然后选择一个最优特征，按此特征将数据集划分成若干子集，使得每个子集尽可能纯净（易于分类）。如果某个子集已能被基本正确分类，则在该处创建叶节点，结束划分；否则，对该子集继续选择新特征进行递归划分，直到所有子集被基本正确分类或没有更多可用特征为止。

虽然这样生成的决策树对训练数据可能有很好的分类效果，但往往对未知的测试数据表现不佳，即容易出现过拟合。为提高模型的泛化能力，需要对决策树进行剪枝，通常是自下而上地去掉过于细分的叶节点，将其回退到父节点或更高节点，并将父节点改为新的叶节点，从而简化树结构，增强模型对未知数据的适应能力。

特征选择与决策树生成

信息熵

信息熵（Entropy）是表示随机变量不确定性的度量，设X是一个取有限个值的离散随机变量，其概率分布为：

信息增益与 ID3

ID3 算法在决策树各个节点上应用信息增益选择特征，递归地构建决策树。具体方法是：从根节点开始，计算所有可能的信息增益，选择信息增益最大的特征作为节点特征，由该特征的不同取值建立子节点，再依次对子节点进行上述操作，直到所有特征信息增益均很小或无特征可选为止，最终生成一颗决策树。

知识梳理

#大模型 #机器学习核心理论

深度学习总结上一篇

PyTorch 安装运行报错下一篇